In the US we have many options for sending money around: there's the traditional cash, check, credit card, bank transfer, etc., and then there's PayPal, Venmo, Square, Wallet, etc. In poorer countries, however, if you want to send money to someone in another city your best option is often to send cash on a bus. In 2007 Safaricom introduced M-Pesa in Kenya, where it has been very successful. Can we get an estimate of how valuable M-Pesa has been?

In The long-run poverty and gender impacts of mobile money (Suri and Jack 2016) they try to figure out the effect of the M-Pesa rollout on per-capita consumption. They argue that from 2008 to 2010, when M-Pesa was just getting started, new agents were distributed effectively randomly. [1] Then they look at how areas that were close to M-Pesa agents in 2008-2010 compare to ones that weren't, and argue that this difference represents the effect of having access to M-Pesa.

They find that having access to M-Pesa raised log [2] per-capita consumption by 0.012 (n=1593, standard error=0.005, Sidak-Holm p=0.04). (EDIT: this is an underestimate; see update below.) The reason to care about log consumption is that the more money you have the less valuable additional money is, and this relationship is approximately logarithmic (though it might fall off even more sharply). So by averaging log consumption over all the people in their sample we're getting a rough approximation of how much better M-Pesa access made people's lives.

What does a 0.012 increase in log per-capita consumption look like? Here's a table:

per-capita consumption	change
$50,000	$603
$25,000	$302
$10,000	$121
$5,000	$60
$2,500	$30
$1,000	$12
$500	$6
$250	$3
$100	$1

To get a comparison, another way to increase someone's consumption would be to just give them money. GiveDirectly is currently the best option for doing this, and on average GiveDirectly gives $288 per-person to recipients with an annual consumption of $238, a log-increase of 0.79. This is 66x the 0.012 log-increase for M-Pesa availability. GiveDirectly is about 80% efficient, so getting someone $288 costs about $360. So, very roughly, giving someone access to M-Pesa one year earlier is about as valuable as donating $5.45 to GiveDirectly. [3]

While M-Pesa was very successful in Kenya, its expansion to other markets has been slow. Improving M-Pesa's expansion, or starting a competitor that can expand faster, could be very valuable. For example, the population of Ethiopia is 94M, so getting mobile money available in Ethiopia a year earlier would be about as good as donating $500M to GiveDirectly. [4]

This is a very rough analysis, and as it is essentially a multiplicative chain errors anywhere along the chain are magnified. For example, two errors in the first version of this post moved the final estimate by 2.3x and 1.5x respectively. This estimate is nowhere near as robust as, for example, GiveWell's estimates for GiveDirectly or the AMF, and those are still very uncertain. Still, it suggests deploying mobile money is an extremely promising intervention, competitive with the top global poverty interventions.

Update 2017-01-01: Tavneet Suri, corresponding author of the paper I'm drawing on here, responded to my question about the interpretation of cell 1 in table 1. Above I interpret it as the effect of having an M-Pesa agent within 1km, but it's actually the effect of having one additional M-Pesa agent within 1km. Since the average number of M-Pesa agents within 1km was ~9, naively we'd expect this to mean the effect of M-Pesa is 9x what I estimated above. But since the first M-Pesa agent is probably much more valuable than the tenth, and their sample mostly didn't include this no-access-to-access transition, the true effect is probably more than 9x. On the other hand, this is kind of big, maybe implausibly so. Instead of a ~1% increase, we're talking about more like 20%. Could M-Pesa really have made Kenya that much richer?

[1] On the other hand, after 2010 they believe there was a systematic effort to expand in places with higher demand. Overall, this is one of the weakest parts of this analysis: if places that got agents earlier were more actually more economically dynamic then it wouldn't be at all surprising to see greater consumption growth there.

[2] The paper doesn't say what base they're using for the log, but I'm assuming here that it's e: natural log is standard in economics. Additionally, in Table S1 of the supplement they give both "Daily per Capita Consumption" and "Log Daily Per Capita Consumption", and the particular numbers they have rule out a base as large as 10. In a draft of this post I had initially assumed log10: thanks to Rob Wiblin for catching this.

[3] My model of this is that you can either wait and get the consumption boost from mobile money eventually, or you can do something to make it happen sooner. If we take a window long enough to include the eventual deployment of mobile money I would expect to see something like:

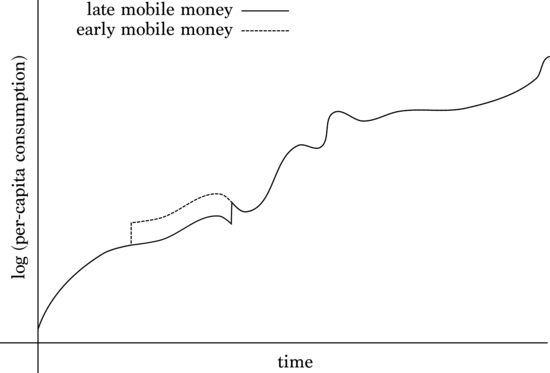
The solid line represents the path the average log(per-capita consumption) would take, with a jump at the eventual introduction of mobile money, while the dashed line represents moving that jump forward in time. So the benefit is the area between the two curves: how much better mobile money is for people, multiplied by how much you can accelerate it.

[4] Or donating $105M to the AMF, according to GiveWell's cost-effectiveness estimates.